Implicaciones de las sinergias en la valuación de activos y el cumplimiento del principio arm´s length
Ha sido muy habitual considerar que los precios de mercado, e incluso la aplicación de métodos “justos” de valuación de activos con mucha aceptación, son suficientes para cumplir con el principio arm´s length. Sin embargo, esto no es necesariamente así, pues hay fenómenos económicos, como las sinergias que tienen implicaciones peculiares.
Las sinergias implican que la interacción de activos, que bien puede darse por la coincidencia de su presencia en la misma organización, conlleve una generación de valor conjunta mayor a la suma de la generación de valor de cada activo de forma individual sin interactuar entre sí.
En términos de una transacción del activo, esto podría significar que la aportación de valor que tendría para la entidad que lo compra no fuese la misma cantidad que pierde la entidad que lo vende.
Respecto a la valuación del activo en cuestión, un camino muy aceptado es el del valor presente de los flujos futuros descontados, donde el principal problema es la identificación de las utilidades de la empresa que le serian atribuibles al activo analizado.
Para simplificar este punto, la herramienta del valor de Shapley nos puede ayudar a determinar las utilidades que “justamente” le serian atribuibles a un activo específico localizado en una compañía.
El valor de Shapley es un método de distribución de riqueza en la teoría de juegos cooperativos en el supuesto de que todos colaboran formando una gran coalición. Es una distribución “justa” en el sentido de que es la única distribución con ciertas propiedades deseables (eficiencia, asimetría, linealidad y jugador nulo).
Dado un grupo N (de n jugadores) y una función υ : 2N → R con u ∅=0, donde ∅ denota conjunto vacío. La función v que asigna subconjuntos de actores reales se llama función característica. La función v tiene el siguiente significado: si S es una coalición de jugadores, entonces v(S), llamado el valor de la coalición S, describe la suma total de los pagos a los miembros de S que se puede obtener por dicha cooperación.
De acuerdo con el valor de Shapley, la cantidad que el jugador i obtiene durante un juego de coalición (v,N) es:
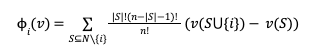
Donde n es el número total de jugadores y la suma se extiende sobre todos los subconjuntos de N que no contiene el jugador i.
Ejemplo.
Supongamos que tenemos 3 jugadores ({ a,b,Δ,}) donde a son el conjunto de activos alojados en A (excepto Δ ) y b son el conjunto de activos alojados en B, mientras que Δ es un activo difícil de valuar.
Inicialmente el activo Δ se encuentra en propiedad de A y se analiza su venta a B, por lo tanto, la estimación de la utilidad “justa” correspondiente al activo Δ es:
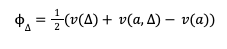
Siendo f∅=w, f:R→R una función donde ∅ es la utilidad anual de un activo y w el valor presente del activo.
El precio del activo Δ sería entonces:
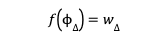
Implicaciones Arm´s length.
Sin embargo, A no debería estar dispuesto a vender el activo Δ a un precio menor a f(v(aΔ)-v(a)), tal que de otra forma no compensaría la pérdida de utilidades para A por dejar de explotar del activo Δ.
Entonces, en caso de que se cumpliera que v(Δ) < v(a,Δ) – x(a) que no habría ningún impedimento para que esto ocurra, w no sería arm’s length a pesar de ser un precio “justo” al no ser un precio por el cual el propietario del activo estuviera dispuesto a vender.
Además, en caso de que se cumpliera que v(a,Δ)-(v(a)>v(b,Δ)-v(b), la curva de contrato entre A y B seria ∅. Es decir, no habría ningún precio posible por el cual se efectuara la transacción ya que en cualquier precio ya sea A, B o ambas, empeorarían su situación inicial, lo cual no cumpliría el principio arm´s length.
Lo descrito anteriormente nos lleva a reflexionar que si bien la prioridad del marco de precios de transferencia es el cumplimiento arm´s length puede ser habitual que la falta de información en el análisis conlleve el riesgo de no tener manera de demostrar la existencia o hallar precios arm´s length pero que de igual forma los precios de mercado asi como los precios “justos” teóricos pueden ser una alternativa aceptable sobre todo de cara a la práctica del análisis de precios de transferencia.
JCG

